Research

Understanding the extremely rich macro- and mesoscopic phenomenology of matter in terms of microscopic physical laws has always been one of the most fascinating endeavors of science. Improvements in this understanding based on quantum mechanical laws have led to undreamt-of technological advances in many areas, and in recent years even former visions such as quantum computing seem to have come within reach. The mission of the CRC is to contribute to this scientific enterprise at the level of its mathematical foundations.

The CRC is focused on the mathematical analysis of models from condensed matter physics, where the collective behavior of a large number of interacting components such as particles or spins leads to a diverse and technologically relevant phenomenology. While the mathematical equations that make up the microscopic quantum models are mostly well understood, the task of extracting useful information from them and linking them to collective phenomena at a meso- or macroscopic level still pushes the limits of current mathematical technology.

The mathematical understanding and harnessing of correlations is the unifying theme of the CRC. Different facets and types of correlations and entanglement in many-body quantum systems will be addressed from different perspectives. Each project either contributes to the analysis of correlations in specific classes of models, or proves the emergence of collective phenomena of interest and develops improved numerical algorithms based on a thorough understanding of the correlations, or both.

Projects

Projects in Group A will improve our understanding of exact many-body states of fundamental microscopic models, while projects in Group B will use this understanding to develop and improve effective descriptions. However, the division we have chosen is not sharp by any means, as several projects deal with both aspects and there are strong links between projects from A and B on at least two other levels, namely in terms of mathematical techniques and in terms of the physical nature of the system or phenomenon. Links on the level of mathematical areas and techniques are indicated in the figure below.

                 

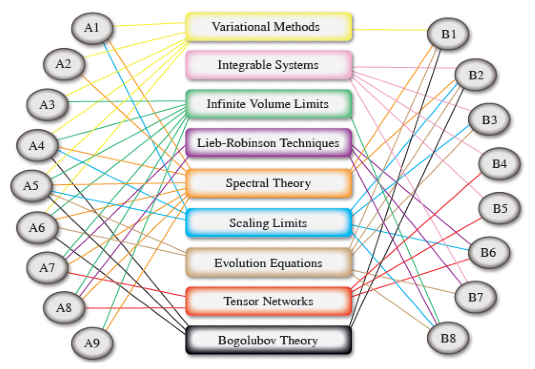
A — Analysis of Low Energy States in Highly Correlated Quantum Systems
A1 Large Quantum Coulomb Systems (Frank, Nam, Solovej)
A2 Rigorous Approximations for Fermionic Kinetic Energies (Frank)
A3 Decay of Correlations in Continuum Particle Systems (Heydenreich, Jansen)
A4 The Correlation Energy of Many-Body Bose Systems (Hainzl, Schlein, Triay)
A5 The Correlation Energy of Many-Body Fermi Systems (Hainzl, Nam, Seiringer)
A6 Mathematical Challenges in the BCS Theory of Superconductivity (Frank, Hainzl, Seiringer)
A7 Low-Energy States and Spectra of Quantum Hall Systems (Lemm, Warzel)
A8 Finite-Size Criteria for Spectral Gaps in Quantum Lattice Systems (Lemm, Warzel)
A9 Localization for Very Sparse Erdős–Rényi Random Graphs (Erdős, Heydenreich, Müller)

B — Effective Descriptions and Numerics of Complex Quantum Systems
B1 Norm Approximation for Interacting Many-Body Fermi Gases (Pickl, Schlein)
B2 Derivation of Nonlinear Quantum Boltzmann Equations (Nam, Spohn)
B3 Hydrodynamic Equations for Integrable Many-Body Systems (Mendl, Spohn)
B4 Numerical Gaussian-Based and Tensor-Network Methods in Quantum Dynamics (Lasser, Lubich)
B5 Numerics for Wigner–Weyl Methods in Many-Body Quantum Dynamics (Lasser, Mendl)
B6 Complexity in Many-Body Quantum Systems (Christandl, König, Wolf)
B7 Markovian Dynamics in Many-Body Quantum Systems (Capel, Rouzé)
B8 Local Stable Gaps and Response in Interacting Many-Body Quantum Systems (Capel, Teufel)