A2 Rigorous Approximations for Fermionic Kinetic Energies
Project Leaders

Researcher
Summary
The famous Lieb–Thirring (LT) inequality [LT75] bounds the fermionic kinetic energy from below by a functional of the one-particle density only. This allowed Lieb and Thirring to prove the stability of matter with constants in the physical range, and lead to a better understanding of Density Functional Theories [HK64; L83]. The LT inequality and other semi-classical trace inequalities like, for instance, the Kato–Seiler–Simon inequality, are an essential tool in the mathe-matically rigorous study of large atoms and molecules, as well as in the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity. While these problems concern rather different physical models, their mathematical analysis relies, in part, on similar techniques of semiclassical analysis with minimal regularity, which is where universal spectral inequalities like the LT inequality come in.
A notoriously open problem in this area, the Lieb–Thirring Conjecture, is the question of the optimal constant in the LT inequality. To be precise, it is conjectured [LT75; L83] that in dimensions d ⩾ 3, for all N-body fermionic wave functions ΨN with corresponding one-body density ρψN one has
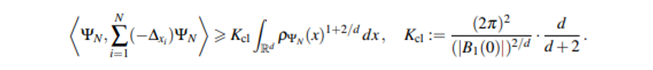
The constant Kcl is the one obtained by the Thomas–Fermi approximation. In the dual formulation, bounding the total energy of non-interacting fermions in an external potential, the conjecture says that the corresponding phase-space energy is not only asymptotically correct in the semiclassical limit (knownas Weyl’s Law), but is a universal lower bound for finite parameters as well.
A rigorous lower bound, where the classical constant is replaced by another universal constant, was first proved in [LT75]. In the last few years, there has been substantial progress towards the resolution of this conjecture. For instance, the best known estimate for the constant was established recently in [FHJN21*]. Moreover, a lower bound with the sharp semiclassical constant plus an error term of gradient type has been established [N18] by a many-body localization method.
Progress in a different direction was made in [FGL21*a] where, on the one hand, the dual form of the Lieb–Thirring conjecture on the γ-moment of eigenvalues was disproved for certain values of γ and, on the other hand, a new optimality scenario was suggested involving a phase transition with respect to γ. In a certain range of γ’s, a “solid” phase was conjectured with the emergence of nontrivial periodic structures. Numerics supports this new conjecture. This suggests to view the Lieb–Thirring conjecture as a problem in statistical mechanics and might open up a new line of attack on this long-standing problem. The purpose of this project is to study the total kinetic energy of fermionic many-body quantum systems. One of our main goals is to develop new approaches to the Lieb–Thirring conjecture, which says that the fermionic kinetic energy is controlled by the one-particle density semiclassical approximation. In the dual formulation, we will investigate trace asymptotics for magnetic Schrödinger operators with low-regularity fields.
[LT75] E. H. Lieb and W. E. Thirring. Bound for the kinetic energy of Fermions which proves the stability of matter. Phys. Rev. Lett. 35 (1975), 687–689.
[HK64] P. Hohenberg and W. Kohn. Inhomogeneous electron gas. Phys. Rev. 136 (1964), B864–B871.
[L83] E. H. Lieb. Density functionals for Coulomb systems. International Journal of Quantum Chemistry 24 (1983), 243–277.
[FHJN21*] R. L. Frank, D. Hundertmark, M. Jex, and P. T. Nam. The Lieb-Thirring inequality revisited. J. Eur. Math. Soc. (JEMS) 23 (2021), 2583–2600.
[N18] P. T. Nam. Lieb-Thirring inequality with semiclassical constant and gradient error term. J. Funct. Anal. 274 (2018), 1739–1746.
[FGL21*a] R. L. Frank, D. Gontier, and M. Lewin. The nonlinear Schrödinger equation for orthonormal functions II: Application to Lieb-Thirring inequalities. Comm. Math. Phys. 384 (2021), 1783–1828.

